Module: Threshold_Global

Description:

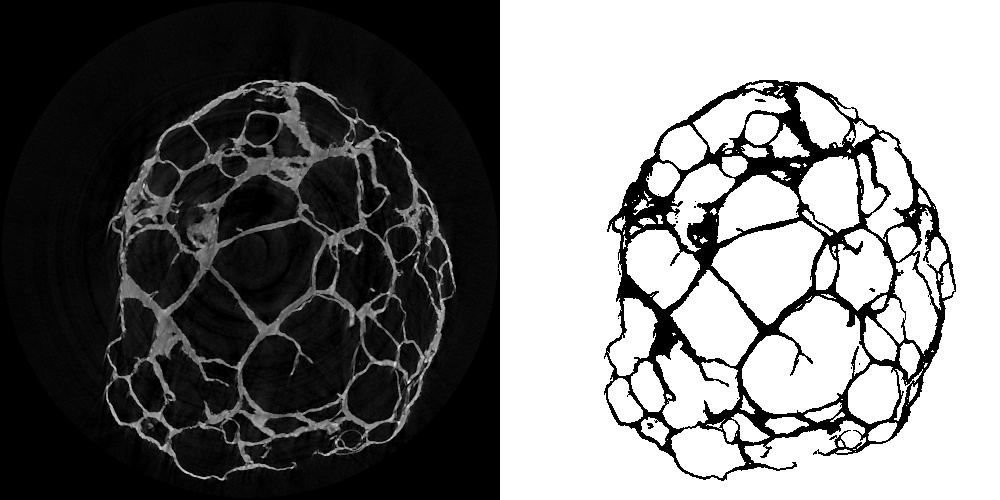
Illustration of the binarisation procedure. Original image is on the left, result on the right, in which the object is defined as black, and background as white.

Notes

• No automatic method to set the threshold was developed with an equality comparator in mind (= or ≠). More specifically, the methods were implemented with the ≥ operator (< would produce the same result, and in most cases, so will the other two ordering operators).
• If a histogram method is selected and there's a histogram connected at the input, then the module will use that histogram (provided it's valid). If not, no matter if a histogram has already been computed by the module (at the output), it will always recompute the histrogram.

Connections:

Image

ROI

Mask

Histogram

Ports:

Threshold

Comparison

Values

Automatic choice of threshold

Auto

AutoHisto

Peaks

• Compute Cumulative Distribution Function (CDF)
• Smooth CDF: using an averaging window of given size (an odd number).
• Subtract smoothed CDF from CDF: this is equal to the derivative of the smoothed histogram (see appendix in cited paper. And I checked, it works...). The result is called the Peak Detection Signal (PDS).
• Find peaks: in the PDS, a peak is defined by three values. The peak start is when a negative crossover is found (going from positive to negative values). The peak maximum is the following positive cross-over. The peak end is the local maximum between the start of the current peak and the start of the next one.

Implementation and customisations

• Histogram and CDF: starting with table Histogram, the first column, Greylevel, gives the greylevel of the center of the bin, the second column, Number, is the number of pixels in that bin (i.e. closer to that bin's center value than any other bin center value), and the third, Cumulative, is the sum of the number of pixels in that bin and the number of pixels in all preceding bins.
• Smoothed CDF: the half-size of the averaging window for the smoothing of the CDF is defined by the N/2 value set in this port. The size of the window will then be (N/2)*2+1=W (like that it's always an odd number). The cited paper does not explicitely describe what happens on the CDF border, where the averaging window only partially overlaps the CDF. It implies zero-padding, but when doing it that way, the end part of the PDS shoots out the roof, and when merging peaks in the final part of the method (i.e. finding the biggest of the maxima), it always chooses the greylevel of that last peak's maximum, which is bad. So instead of systematically dividing the sum of the PDS values in the windows by W, I divide that sum by the number of values in that window (e.g. N/2+1 when at the CDF border). That way, the subtraction of smoothed CDF from CDF will not shoot up. The smoothed CDF is in column four, Averaged.
• PDS: or the difference between the two last columns, is in the fifth column, PDS
• Peaks: the set of peaks, defined by their start, end, and maximum, are found and stored in the second table, called Peaks, in the first three columns, intelligently named Start, End, and Maximum. Note that in these columns it isn't the greylevels that are stored, but the row indices to the corresponding greylevel (starting at 0). In other words, a value of i refers to the greylevel at row i+1 in table Histogram.
• Merge peaks until two remain: the paper suggests that when a fixed number of quantisation levels is sought (in our case, we want two), then the averaging window should first be automatically adjusted before some final merging is applied with the closeness criterion. I found after a few tests that changing the averaging window size would alter the result in a bad way, more often than not. So to simplify the process, I find the two consecutive peaks that are farthest apart using that closeness criterion, and merge with the left one all peaks before it, and merge with the right one all peaks after it. The fourth column in the Peaks table, called Index, is the row number (again, starting at 0) to the maximum of that merged peak. This means that you can see where the pair farthest apart is and how the peaks were merged (all peaks with the same value have been merged). Note that this value is a row number to the Maximum column, itself a row number to the Greylevelcolumn in the first table. It's like the movie Inception, but with arrays instead of dreams.
• Find and set threshold value: contrary to the paper, I set the threshold value to the average of the greylevels of the maxima of the two final peaks.

Notes

• The N/2 value doesn't need to be huge (the default seems sufficient for typical applications).
• Even if plenty of peaks are found, the merging process seems fairly robust.

Otsu

This method is an discrete analog of Fisher's linear discriminant², and was introduced by the namebearer Nobuyuki Otsu in a hugely cited paper³.

It finds the grey-level threshold θ_Otsu such that the variance between the two classes of pixels defined by that threshold is maximum. In maths it can be written as:

• p(k) is the normalised histogram
• μ is the average grey-level
• μ₀ is the average grey-level for all pixels that have a grey-level < θ
• μ₁ is the average grey-level for all pixels that have a grey-level ≥ θ

Bayesian

This method supposes that the image is made up of two classes of greylevels each having a Gaussian distribution. In other words, we suppose that the histogram is a union of two Gaussians. A (normalised) Gaussian can be defined by an expected value μ and variance σ², and is written g(x) = (1/√(2π)σ)exp(-(x-μ)²/σ²). This can also translate as the probability of observing x in such a distribution.

The idea is that a threshold value defines two groups, one containing all pixels with a strictly smaller greylevel, and with greater or equal greylevel. From each, the mean and variance are computed (μ₀, σ₀, μ₁, σ₁) and define the Gaussian distribution for each group. In this framework, the optimal threshold θ would have an equal probability of belonging to either group, i.e. g₀(θ) = g₁(θ).

In practice, we test only the values defined in the histogram, and we won't find a threshold θ such that g₀(θ) is perfectly equal to g₁(θ). What is done instead is that for each threshold candidate x, the two Gaussians are determined and (i.e. the means and variances are computed), and g₀(x) and g₁(x) are calculated. We then compute the ratio of the largest by the smallest: max(g₀(x), g₁(x))/min(g₀(x), g₁(x)). From all the candidates defined by the histogram bins, we choose the one with the ratio closest to 1 as θ.

Notes

• Creates columns Prob_0 and Prob_1 in the resulting spreadsheets, containing g₀(x) and g₁(x). Is the verbose command is used, also created columns containing the means and variances.
• I didn't find any references describing this method, so I did it myself. If I got it wrong, please let me know.

AutoIter

Isodata

• Set arbitrary initial threshold th, here as the middle of the grey-level range.
• Compute means μ₀ and μ₁, the mean grey-levels of pixels belonging to each group, defined by the threshold th and comparator set in the Comparison port.
• Set new threshold th' = (μ₀ + μ₁)/2, if th'≠th then set th←th' and repeat.

Porosity

Note on the iterative methods

Commands:

verbose

create

Scripting:

	set B [create Binarise]
	$B Image connect $INPUT_IMAGE; $B fire
#	$B Threshold setValue $THRESHOLD; $B Comparison setValue 3
	$B Auto setValue 2; $B fire
	$B Iter_Method setValue 3 1; $B fire
	set OUTPUT_IMAGE [$B create]

References: