Module: Fit_Cylinder

Description:

Finds the best cylinder fit from a set of horizontal circles (i.e. defined on the (Oxy) plane) by their respective centres and their radii. It computes a linear regression from the circles' centres and averages the radii. The output is of type HxLineSet storing one segment which defines the cylinder's axis, and a data value which stores the cylinder's radius. The axis is determined as follows (S being the set of circle centers in 3D to regress to a line L) :

Project S onto two easy planes (here we arbitrarily chose (Oyz) and (Oxz)), then a linear regression on those two planes.
The two lines found in the two planes are extended to 3D giving two planes respectively perpendicular to the former ones. Their intersection gives us L.

The radius of the cylinder is simply the average radius of the circles.

A refinement process can be used to remove spurious circles that shouldn't be used in the regression. The refinement parameter is a fraction k of the distance to L of the furthest point of S. It acts as a threshold in the following iterative manner to find the subset S' of points to keep for the regression:

Set S' = S.
Regress S' to find L.
Find the point x ∈ S such that its distance d(x,L) to the line L is maximum.
Find the points x' ∈ S' furthest from L. If d(x',L) > k.d(x,L), then remove x' from S' and go back to step 2.

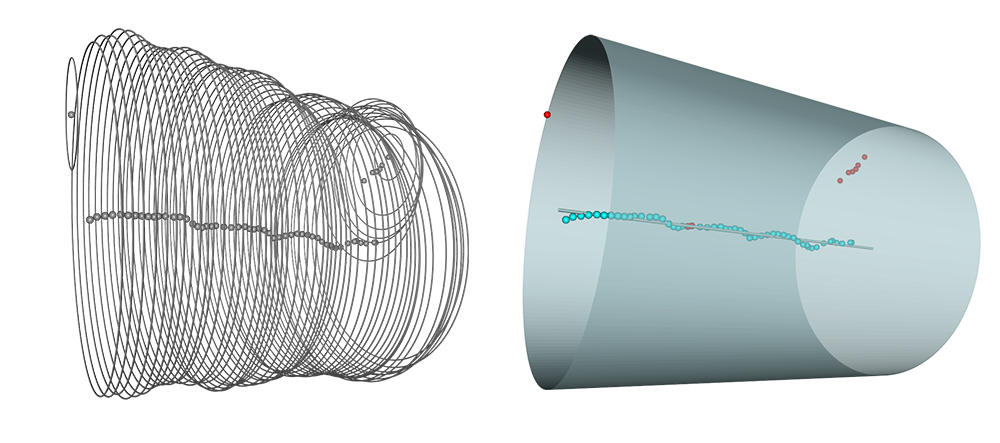Typical example: on the left is the set of circles defined from encircling the points of an object on each plane of the image (done with the module Encircle and visualised with Draw_Circles). On the right is the output cylinder with k = 0.1 (visualised using Draw_Cylinder). Note that the points in red are those not in S' (there are two reds in the centre that seem to be right on L, but they're actually pretty far behind).

NOTES:

Once a point has been removed from S', it will never be added back again, even if subsequent regressions L move back close to it.
To retrieve in a script the two points that define L and radius of the output cylinder, the TCL code can look something like this (Cyl being the output): Cyl getPoint 0; Cyl getPoint 1; Cyl getData 0 0
I implemented the refinement procedure backwards... The reference here is the biggest outlier, and outliers can vary wildly from image to image, so having a robust reproductible processing accross multiple datasets is not possible with this refinement. It should be a factor of the smallest distance. Or simply a number or fraction of the number of points...

Connections:

Circles

[required]
The input circles, defined in a class HxCluster, in which the point coordinates are the circles' centres, and the object contains a data column with the name radii which contains the circles' radii.

Ports:

Refinement

Provides the fraction k described above.

Option

In order to view the points in S', this option adds a data column named kept (if it doesn't already exist) in the input, and set to 1 or 0 whether the corresponding point is in S' or not, respectively.

Action button

Push this button to start the projection.

Commands:

Additional options can be accessed when typing in the console Fit_Cylinder COMMAND_NAME. Typing the command again usually reverts back to original settings.

`verbose`

Displays timing information after the computation. Retype to hide info.

`create`

Runs the computation. Returns the name of the output, so it can be used in a script, such as set RESULT [Fit_Cylinder create].